The Max Pooling Layer

Introduction

In the previous article, we saw what the learning structure of the $ Convolution $ $ layer $ was.

In this article we discover a new simple $ layer $ with no weights at all: the $ Max $ $ Pooling $ $ layer $.

The Max Pooling Neural Structure

Let us talk about the following setup:

• $ L^{k-1} $ is a $ Convolution $ $ layer $ with 2 output channels
• $ L^{k} $ is an $ Max $ $ Pooling $ $ layer $

The principal objective of the $ Max $ $ Pooling $ $ layer $ is to reduce the size of the different input channels. Except for this dimensional reduction, it preserves the same structure as its previous $ layer $.

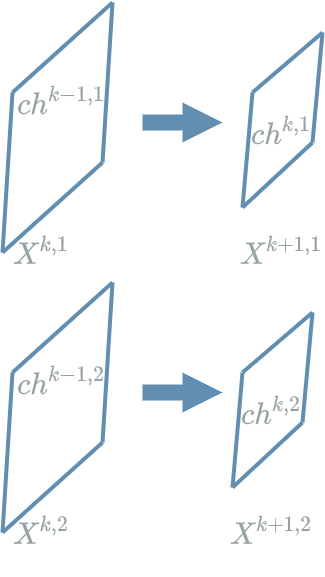
Let us now see how the $ Max $ $ Pooling $ $ layer $ works when its goal is to divide the size by 2.

Let us take one output neuron example:

\[\begin{align} ch^{k,1}_{1,1} &= max^{k,1}_{1,1} \\ &= max(ch^{k-1,1}_{2,2}, ch^{k-1,1}_{2,3}, ch^{k-1,1}_{3,2}, ch^{k-1,1}_{3,3}) \\ \end{align}\]

Forward Pass

Just apply the operation described in the previous paragraph.

Backward Pass for the Learning Flow

Let us focus on the back propagation of the learning flow for the neuron $ \delta^{k,1}_{2,2} $:

\[\delta^{k,1}_{2,2} = \frac{\partial Loss}{\partial X^{k,1}_{2,2}}(ch^{k-1,1}_{2,2})\]

The interesting variable is $ X^{k,1}_{2,2} $. Let us find its impacts on the $ Loss $ function.

If we look back at the forward pass, there is only one output neuron susceptible of using the considered variable, it is: \(ch^{k,1}_{1,1}\) (appearing as \(max_{1,1}\) in this diagram).

Because of the $ max $ formula, there is still a chance that \(ch^{k,1}_{1,1}\) has not used \(X^{k,1}_{2,2}\) at all. In this case, we will have:

\[\boxed{ \delta^{k,1}_{2,2} = 0 }\]

The only way that $ \delta^{k,1}_{2,2} \neq 0 $ is that:

\[max^{k,1}_{1,1} = ch^{k-1,1}_{2,2}\]

In that case we will have:

\[\boxed{ \delta^{k,1}_{2,2} = \delta^{k+1,1}_{1,1} }\]

What appears is that for every “cell” in the previous diagram, there is only one learning flow that will not be null during the backward pass.

In fact this is logic when we recall that during the forward pass each output neuron has used only one input neuron: the maximal neurone in the considered “cell”

Conclusion

We have seen the neural structure for the $ Max $ $ Pooling $ $ layer $. In the next article, we will work on a new $ layer $: the $ Normalization $ $ layer $.